Вопрос 1 ТАУ
Каноническое
уравнение системы управления во временной и частотной области : назначение , применение.
Рассмотрим колебания груза на пружине
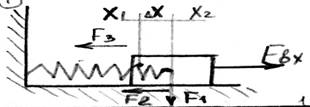
Силы действующие на объект: F1-вес; F2- сила трения; F3- сила сопротивления движению; Fвх- сила действ на тело
F1=mg
F2=kтрN1
F3=kпрΔx
Все выходные сигналы: ![]()
![]()
Рассмотрим электрическую систему
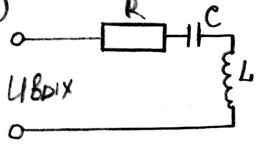
![]()
![]()
![]()
![]()
![]()
На основании 2х математических моделей физической и электрической системы можно сделать вывод: что совершенно разные по природе явления описываются одинаковыми уравнениями. Таким образом все явления можно записать одним уравнением, которое называется каноническим(во временной области)
![]()
Главная цель канонического уравнения: проверка физической реализуемости системы
Условия физической реализуемости технического устройства
1. Степень полинома правой части канонического уравнения должна быть меньше степени полином левой части канонического уравнения m>n
Каноническое уравнение в частотной области? Т.е необходимо его преобразовать по Лапласу:

тогда
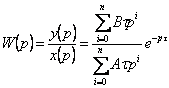
Вопрос 2 ТАУ.
Критерий Найквиста-Михайлова
Критерий Найквиста-Михайлова предназначен для исследования устойчивости замкнутых систем автоматизации систем управления по характеристикам разомкнутых систем.
Критерий Найквиста-Михайлова: Если годограф вектора АФХ разомкнутой системы при изменении частоты от 0 до ∞ не охватывает точку с координатами (-1;0) в плоскости комплексных переменных, то замкнутая система управления будет устойчивой. Если годограф вектора проходит через точку (-1;0) то САУ считается на границе устойчивости.
а)
y x y
![]()
![]()

y W0 Wp W0![]()

б)
y x Wp
Разомкнутая система – это система управления в любом месте.
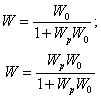 возмущение подается на вход регулятора
возмущение подается на вход регулятора
![]() характеристическое уравнение замкнутой системы
характеристическое уравнение замкнутой системы
![]() решив его, найдем
корни и сможем принять решение об устойчивости. Т.к. уравнение векторное, то
решение графическое если уравнение отрицательное, то векторы WpW0 будут
поворачиваться и совпадать с единичным вектором (-1) и если он больше единичного вектора, то корни
будут действительными.
решив его, найдем
корни и сможем принять решение об устойчивости. Т.к. уравнение векторное, то
решение графическое если уравнение отрицательное, то векторы WpW0 будут
поворачиваться и совпадать с единичным вектором (-1) и если он больше единичного вектора, то корни
будут действительными.

Система уравнений в замкнутом состоянии будет устойчива, если годограф вектора АФХ разомкнутой системы не охватывает точку (-1;0) в плоскости комплексного переменного
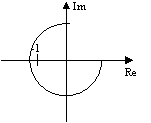
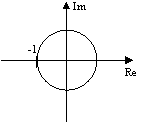

Устойчивая неустойчивая
Для синтеза систем управления данный критерий, имеющий определенное значение по тому, что это единственный критерий который регламентирует условия нахождения системы на границе устойчивости.
Преимущества критерия:
1. Единственный критерий, который предназначен для синтеза САУ
2. Критерий позволяет использовать при синтезе новых систем управления другие критерии
3. Может быт использован для анализа САУ
Недостатки:
Сложность принятия решений (возможно только аналитическим путем для синтеза; для анализа графическим)
Необходимость применения аналитических выражения для разомкнутых систем управления
Вопрос 3 ТАУ.
Методы
исследования свойств объектов управления
При исследовании свойств объекта применяются либо экспериментальные, либо аналитические методы.
Аналитические – это приемы исследования математических моделей.
Недостатки :
1. Очень большие упрощения объектов при составлении мат. моделей
2. Сложность и громоздкость получения конечных конкретных результатов
3. Все конечные результаты требуют экспериментального подтверждения. Тем не менее при проектировании новых САУ где объектами управления являются новые объекты необходимо использовать новые мат модели.
Экспериментальные приемы и методы – это приемы и методы исследования свойств объекта основанные на нанесении типовых возмущающих воздействий.
Делятся на две группы:
1. активные методы, которые предполагают инициативное нанесение возмущений на вход;
2. Пассивные методы, которые предполагают наблюдение за поведением объекта в течении длительного времени и обработку этих наблюдений.
Пример пассивного метода – метод Винера – Химчина; пример активного – метод Симою.
Вопрос 4 Типовые
соединения элементарных звеньев: классификация, структурные схемы, вывод общей
формулы.
Существует
3 основных правила преобразования типовых элементов и 6 правил переноса.
1.
Последовательное соединение передаточных функций.


![]()
![]()
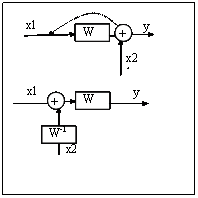
2.
Параллельное соединение передаточных функций.
Для этого соединения
характерно, что один входной сигал разъединяется на
несколько передаточных функций, выходные сигналы которые в свою очередь
соединяются в сумматоре.
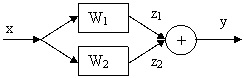
![]()
![]()
![]()
![]()
3.
Встречно параллельное соединение.
Соединение
![]() по принципу обратной связи и подразделяющуюся
на:
по принципу обратной связи и подразделяющуюся
на:
А)
случай, когда вх. Сигнал подается на вход обратной связи выр. через х.
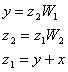
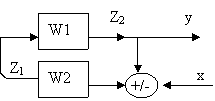
![]() при «+» получим 1-W1W2 при «-» 1+W1W2
при «+» получим 1-W1W2 при «-» 1+W1W2
 Б) случай, когда вх. сигнал подается на вход
примой связи.
Б) случай, когда вх. сигнал подается на вход
примой связи.
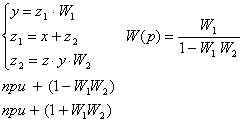
Привила переноса
1.
Перенос звена через сумматор.
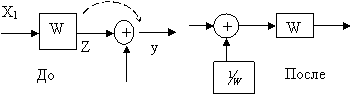 По ходку сигнала. До преобразования
По ходку сигнала. До преобразования ![]() после преобразования
после преобразования ![]()
Вспомогательные правила
1. Перенос узла через сумматор по ходу сигнала: для того, чтобы динамические св-ва системы управления не изменились при переносе узла через сумматор по ходу сигнала необходимо и достаточно во все дополнительные линии, выходящие из узла добавить инверсный сумматор
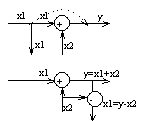
2. перенос узла через сумматор против хода сигнала: для того, чтобы динамические св-ва системы управления не изменились при переносе узла через сумматор против хода сигнала необходимо и достаточно во все дополнительные линии узла, добавить такой же сумматор
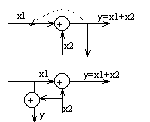
3. Перенос узла через звено по ходу сигнала: для того, чтобы динамические св-ва системы управления не изменились при переносе узла через звено по ходу сигнала необходимо во все вновь введенные линии, выходящие из нового узла добавить инверсное звено.
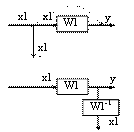
4. Перенос узла через звено против хода сигнала: для того, чтобы динамические св-ва системы управления не изменились при переносе узла через звено против хода сигнала необходимо во все линии, выходящие из нового узла добавить такое же звено.

5. Перенос сумматора через звено по ходу сигнала: для того, чтобы динамические св-ва системы управления не изменились при переносе сумматора через звено по ходу сигнала необходимо во все линии, входящие в сумматор добавить такое же звено.
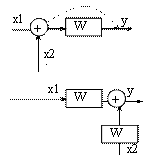
6. Пренос сумматора через звено против хода сигнала: для того, чтобы динамические св-ва системы управления не изменились при переносе сумматора через звено против хода сигнала необходимо в перенесенный сумматор, добавить инверсное звено.
5 ТАУ Интегральные
критерии качества и их применение.
Интегральные критерии – это критерии, которые оценивают качества СУ в статике и динамике
1. Абсолютный критерий качества
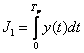
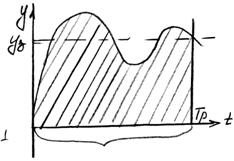
Применяется только для анализа, т.к. при синтезе приводит к большому количеству ошибок.
Чем меньше J1, тем лучше.
2. Модульный критерий качества
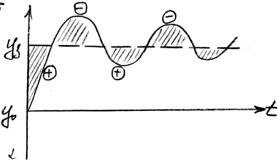
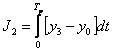
Положительные и отрицательные разности могут друг друга компенсировать и система может быть идеальной, поэтому область применения: анализ СУ
3. Модифицированный модульный критерий качества.

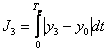
Применяется как для анализа, так и для синтеза (где простые переходные процессы 1, 2-порядка)
4. Среднеквадратический критерий качества.
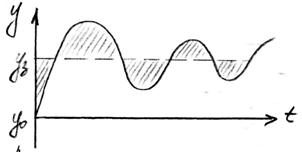
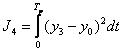
<1 возведение в квадрат уменьшается
>1 возведение в квадрат увеличивается
Основные преимущества
1 Критерий комплексно охватывает практически все критерии качества.
2 Критерий удобен для анализа систем управления, поскольку обладает свойства модульных критериев (2 и 3)
Вопрос 6 ТАУ
Понятие
параметрических функций
Параметрические функции водят специально для упрощения синтеза ПИД-регуляторов. Параметрическая функция существует только у расширенных АФХ. Для расчета ПИД-регулятора используются расширенные АФХ по критерию заданной степени колебательности m.
Расширенная АФХ

Мнимая параметрическая ф-я – это часть расширенной АФХ.
![]()
![]() R- реальная
параметрическая функция.
R- реальная
параметрическая функция.
Реальная параметрическая функция – это часть от реальной части расширенной АФХ.
Расширенная АФХ может быть выражена через параметрические функции
![]() - расширенная АФХ
регулятора.
- расширенная АФХ
регулятора.
Параметрические функции используются для расчета настроечных коэфициенто регуляторов, которые необходимо определить два и более параметров.
Для этого используется плоскость параметрических функций.
Плоскости параметрических функций – это плоскость комплексных переменных с координатами I и R .
I - зависит от к2 и к3 R – зависит от к1 и к3
Фактически это аналог плоскости настоечных коэффициентов.

7 Вопрос Понятие об объекте управления. Основные
свойства объектов.
Объект управления - это техническое устройство которое реализует заданный человеком алгоритм функционирования. Объект представляет собой физическое устройство которое обладает определенным количеством входных и выходных координат.
Основные свойства объектов: самовыравнивание, емкость, запаздывание.
Самовыравнивание
Для чего исследуется:
1. для составления схем управления объектом
2. для выбора типа регулирующего устройства
3. для определения оптимальных настроек регулятора
4. для получения качественных технологических процессов
Основными свойствами являются: самовыравнивание, емкость, запаздывание.
Самовыравнивание объекта характеризует его инерционность и устойчивость. Самовыравнивание называется свойство устойчивости объекта устанавливающегося в равновесное состояние самостоятельно без постороннего вмешательства после изменения его входной величины.
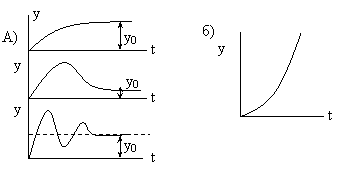
а) самовыравнивание б) Без самовыравнивания
В объектах с самовыравниванием ступенчатое изменение входной величины приводит к изменению выходной величины со скоростью, которая постепенно уменьшается до 0. Это вызвано наличием в объекте внутренних отрицательных обратных связей. Количественная характеристика самовыравнивания – степень самовыравнивания ρ.
ρ- это
отношение изменения входной величины к изменению выходной величины по
достижению объектом равновесного состояния. ![]() Чем больше степень
самовыравнивания тем меньше отклонение выходной величины от первоначального
значения. Нейтральные объекты самовыравниванием не обладают. Для устойчивой
работы требует специального применения регулятора. Чем больше степень
самовыравнивания, тем объект более управляем, причем более простыми средствами
(позиционное регулирование). Емкость присуща всем динамическим объектам. Под
емкостью понимают такое изменение входной величины, которое приводит к
изменению выходной величины на 1 за 1ый отрезок времени
Чем больше степень
самовыравнивания тем меньше отклонение выходной величины от первоначального
значения. Нейтральные объекты самовыравниванием не обладают. Для устойчивой
работы требует специального применения регулятора. Чем больше степень
самовыравнивания, тем объект более управляем, причем более простыми средствами
(позиционное регулирование). Емкость присуща всем динамическим объектам. Под
емкостью понимают такое изменение входной величины, которое приводит к
изменению выходной величины на 1 за 1ый отрезок времени . Чем больше емкость объекта тем более сложный регулятор необходимо
выбирать при управлении им. Запаздывание выражается в том, что выходная
величина объекта начинает изменяться не сразу после внесения изменения, а через
какой-то промежуток времени. τ-время запаздывания.
. Чем больше емкость объекта тем более сложный регулятор необходимо
выбирать при управлении им. Запаздывание выражается в том, что выходная
величина объекта начинает изменяться не сразу после внесения изменения, а через
какой-то промежуток времени. τ-время запаздывания. ![]() . Все реальные объекты обладают запаздыванием, т. к.
изменение потоков вещества или энергии в ТОУ протекает с конечной скоростью.
Запаздывание отрицательное свойство объекта и при автоматизации его стараются
уменьшить: устанавливают датчики , исполнительные механизмы как можно ближе к
ТОУ; использовать молоэнерционные средства автоматизации. По способу
восстанавливать равновесные состояния объекты бывают: нейтральные, устойчивые,
неустойчивые. Эти свойства рассматриваются в зависимости от диф. ура. ТОУ.
. Все реальные объекты обладают запаздыванием, т. к.
изменение потоков вещества или энергии в ТОУ протекает с конечной скоростью.
Запаздывание отрицательное свойство объекта и при автоматизации его стараются
уменьшить: устанавливают датчики , исполнительные механизмы как можно ближе к
ТОУ; использовать молоэнерционные средства автоматизации. По способу
восстанавливать равновесные состояния объекты бывают: нейтральные, устойчивые,
неустойчивые. Эти свойства рассматриваются в зависимости от диф. ура. ТОУ.
Вопрос 8 ТАУ
Критерий устойчивости Раусса. Привести
пример исследования устойчивости САУ данным критерием
Критерии устойчивости Рауса, Этот критерии устойчивости предложен английским математиком Э. Раусом в виде некоторого правила (алгоритма).
В первой строке
табл. 3.1 записывают в порядке возрастания индексов коэффициенты
характеристического уравнения, имеющие четный индекс: ![]() во второй строке — коэффициенты с нечетным индексом:
во второй строке — коэффициенты с нечетным индексом: ![]()
Табл 3,1

Любой ![]() из остальных
коэффициентов таблицы определяют как
из остальных
коэффициентов таблицы определяют как
![]() (3.35) где
(3.35) где
![]() (3.36)
(3.36)
В (3.35) и
(3.36) ![]() — индекс, означающий номер столбца;
— индекс, означающий номер столбца; ![]() — индекс, означающий номер строки.
— индекс, означающий номер строки.
Заметим, что число строк таблиц Рауса равно степени характеристического уравнения плюс единица (п + 1).
После того как
таблица Рауса заполнена, по ней можно судить об устойчивости системы. Условие
устойчивости Рауса формулируется так: для
того чтобы система автоматического управления была устойчива, необходимо и
достаточно, чтобы коэффициенты первого столбца таблицы Рауса имели один и тот
же знак, т. е. при ![]() были положительными:
были положительными:![]() 3.37
3.37
Если не все коэффициенты первого столбца положительны, то система неустойчива, а число правых корней характеристического уравнения равно числу перемен знака в первом столбце таблицы Рауса,
Критерий Рауса особенно удобен, когда заданы числовые значения коэффициентов характеристического уравнения (3.30). В этом случае определение устойчивости можно выполнить довольно быстро даже при характеристических уравнениях высокого порядка.
Форма алгоритма, с помощью которого составляют таблицу Рауса, очень удобна для программирования ЭВМ, поэтому критерий Рауса нашел широкое применение при исследовании влияния на устойчивость либо коэффициентов характеристического уравнения, либо отдельных параметров системы, не очень сложным образом входящих в эти коэффициенты, с помощью быстродействующих ЭВМ.
![]()
Для определения устойчивости системы по коэффициентам этого уравнения составим таблицу Рауса.
(Табл. 3.2)
Табл 3,2

Имеется две
перемены знака коэффициентов первого столбца: следовательно, система
неустойчива, а характеристическое уравнение имеет два правых корня.
9. ТАУ
Математическое описание интегрального звена и его характеристики
1.Мат. модель
 преобразование по Лапласу
преобразование по Лапласу
![]()
2. передаточная функция интегрального звена
![]()
3.Динамичексие характеристики
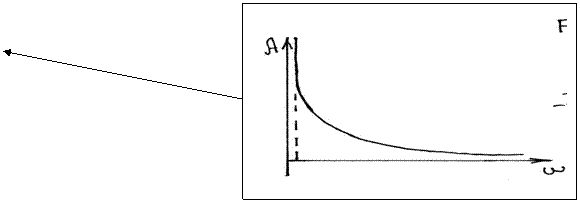 3.1
АФХ
3.1
АФХ 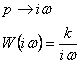
3.2 АЧХ ![]()
3.3 ФЧХ
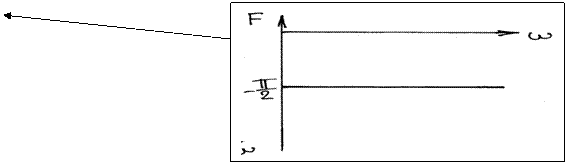
![]()
3.4 График годографа (АФХ)- от-∞ до 0
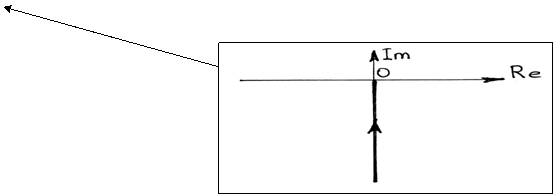
3.5 Переходжный процесс
угол наклона зависит от k
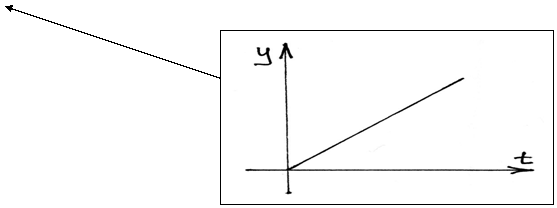
Вопрос 10 ТАУ
Критерий устойчивости Гурвица и его
применение, привести пример исследования устойчивости САУ данным критерием.
Критерий устойчивости Гурвица. А.Гурвицем был разработан алгебраический критерий устойчивости в форме определителей, составляемых из коэффициентов характеристического уравнения системы.
![]()
Из коэффициентов
характеристического уравнения (3,30) строят сначала главный определитель
Гурвица по следующему правилу: по главной диагонали определителя слева направо
выписывают все коэффициенты характеристического уравнения от a1 до аn в порядке возрастания
индексов. Столбцы вверх от главной диагонали дополняют коэффициентами
характеристического уравнения с последовательно возрастающими индексами, а
столбцы вниз — коэффициентами с последовательно убывающими индексами. На место
коэффициентов с индексами больше п (п- порядок
характеристического уравнения) и меньше нуля проставляют нули.
по следующему правилу: по главной диагонали определителя слева направо
выписывают все коэффициенты характеристического уравнения от a1 до аn в порядке возрастания
индексов. Столбцы вверх от главной диагонали дополняют коэффициентами
характеристического уравнения с последовательно возрастающими индексами, а
столбцы вниз — коэффициентами с последовательно убывающими индексами. На место
коэффициентов с индексами больше п (п- порядок
характеристического уравнения) и меньше нуля проставляют нули.
Отчеркивая в главном определителе Гурвица, как показано пунктиром, диагональные миноры, получаем определители Гурвица низшего порядка:
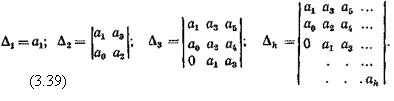 Номер
определителя Гурвица определяется номером коэффициента по диагонали, для
которого составляют данный определитель. Критерий устойчивости Гурвица формулируется
следующим образом: для того чтобы система автоматического управления была
устойчива, необходимо и достаточно, чтобы все определители Гурвица имели знаки,
одинаковые со знаком первого коэффициента характеристического уравнения а0,
т. е. при а0 > 0 были положительными.
Номер
определителя Гурвица определяется номером коэффициента по диагонали, для
которого составляют данный определитель. Критерий устойчивости Гурвица формулируется
следующим образом: для того чтобы система автоматического управления была
устойчива, необходимо и достаточно, чтобы все определители Гурвица имели знаки,
одинаковые со знаком первого коэффициента характеристического уравнения а0,
т. е. при а0 > 0 были положительными.
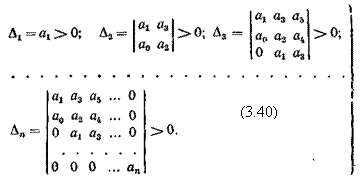 Таким
образом, при а0 >
0 для устойчивости системы не обходимо и достаточно выполнения следующих
условий:
Таким
образом, при а0 >
0 для устойчивости системы не обходимо и достаточно выполнения следующих
условий:
Раскрывая, например, определители Гурвица для характеристических уравнений первого, второго, третьего и четвертого порядков, можно получить следующие условия устойчивости:
1)для уравнения первого
порядка ![]() условия устойчивости
условия устойчивости ![]() (3.41)
(3.41)
2)для уравнения
второго порядка![]() условия устойчивости
условия устойчивости ![]() (3.42)
(3.42)
3)для
уравнения третьего порядка ![]()
![]() (3.43) условия устойчивости
(3.43) условия устойчивости ![]() (3.44)
(3.44)
4)для уравнения четвертого порядка ![]() , условия устойчивости
, условия устойчивости
![]() (3.45)
(3.45) ![]() (3.46)
(3.46)
Таким образом, необходимым и достаточным условием устойчивости для систем первого и второго порядков является положительность коэффициентов характеристического уравнения. Для уравнения третьего и четвертого порядков кроме положительности коэффициентов необходимо соблюдение дополнительных неравенств (3.44) и (3.46).
При п<5 число подобных дополнительных неравенств возрастает, процесс раскрытия определителей становится довольно трудоемким и громоздким. Поэтому критерий устойчивости Гурвица обычно применяют при п<4. При п<5 целесообразно применять формулируемый ниже критерий устойчивости Льенара—Шипара либо при использовании критерия устойчивости Гурвица переходить к численным методам с использованием ЭВМ.
В последнем
столбце главного определителя Гурвица (3.38) отличен от нуля только один
коэффициент ап, поэтому![]() (3.47) Из (3.47), видно, что при ап > 0 для проверки устойчивости системы
достаточно найти только определители Гурвица от А± до
(3.47) Из (3.47), видно, что при ап > 0 для проверки устойчивости системы
достаточно найти только определители Гурвица от А± до![]() Если все определители Гурвица низшего порядка положительны,
то система находится на границе устойчивости, когда главный определитель равен
нулю:
Если все определители Гурвица низшего порядка положительны,
то система находится на границе устойчивости, когда главный определитель равен
нулю: ![]() (3.48)
(3.48)
Последнее равенство возможно в двух
случаях:![]() или
или ![]() . В первом случае система находится на границе апериодической
устойчивости (один из корней характеристического уравнения равен нулю); во
втором случае — на границе колебательной устойчивости (два комплексно
сопряженных корня характеристического уравнения находятся на мнимой оси).
. В первом случае система находится на границе апериодической
устойчивости (один из корней характеристического уравнения равен нулю); во
втором случае — на границе колебательной устойчивости (два комплексно
сопряженных корня характеристического уравнения находятся на мнимой оси).
Используя
критерий Гурвица, можно при заданных параметрах системы принять за неизвестный
какой-либо один параметр (например, коэффициент усиления, постоянную времени и
т.д.) и определить его предельное (критическое) значение, при котором система
будет находиться на границе устойчивости. Следует заметить, что критерий
Гурвица можно получить из критерия Рауса, поэтому иногда критерий Гурвица
называют критерием Рауса — Гурвица.


11. Понятие об
основных законах регулирования: их математичес5ое описание и динамические
характеристики.
Структура типовых регуляторов представляет собой параллельное соединение трех типовых звеньев. Может быть трех типов :
1. пропорциональное звено
2. интегральное звено
3. дифференциальное звено
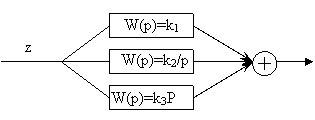

Классификация регуляторов:
а) если k2=k3=0, k1≠0 - регулятор пропорциональный (П-закон регулирования)
б) если K3=0, k1,k2≠0 – пропорционально –интегральный регулятор (ПИ-регулятор)
в) если k1,k2,k3≠0 – пропорционально-интегрально-дифференциальный регулятор (ПИД-закон)
г) если k2=0, k1,k3≠0 – пропорционально-дифференциальный регулятор (ПД-регулятор)
д) если k1,k3≠0, k2=>k3 – пропорциональный регулятор с двойным дифференцированием
ПИ- регулятор самый распространенный (60%)
П-закон
Передаточная функция W(p)=k1

Из передаточной функции выделяем динамические характеристики АЧХ и ФЧХ
ПИ-закон
Передаточная функция W(p)=k1+k2/p
Из передаточной функции выделяем динамические характеристики
АЧХ и ФЧХ

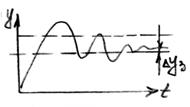
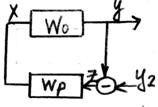
ПИД- закон регулирования
Передаточная функция W(p)=k1+ k2/p+k3p
При синтезе используется критерий Найквиста-Михайлова
Из передаточной функции находим динамические характеристики АЧХ и ФЧХ
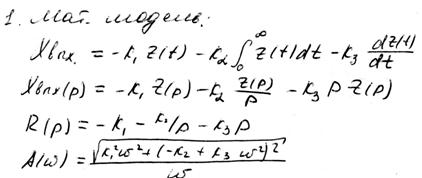
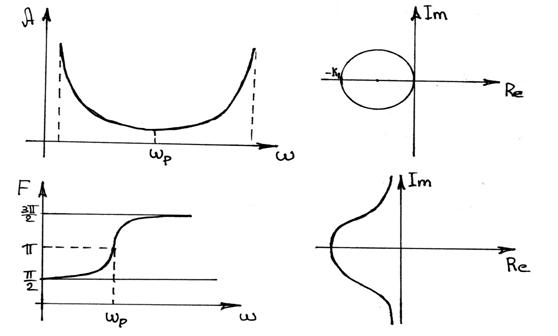
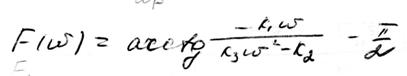
Вопрос 12 ТАУ
Математическое
описание реального дифференцирующего звена и его характеристики.
1. Математическая модель
![]()
преобразование Лапласа: ![]()
2. передаточная функция
![]()
3. Динамические характеристики
АФХ
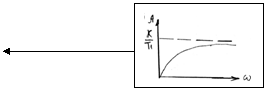
![]()
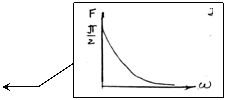 3.1
АЧХ:
3.1
АЧХ:
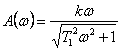
 3.2
ФЧХ :
3.2
ФЧХ : ![]()
3.3 Построение годографа (АФХ)
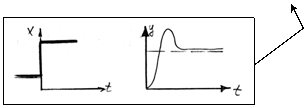 3.4
Переходный процесс (пример:
индуктивность)
3.4
Переходный процесс (пример:
индуктивность)
Вопрос 13 ТАУ.
Экстремальное управление и его особенности
Экстремальными системами регулирования или управления называются такие, которые сами ищут наивыгоднейшую программу, т.е. то значение регулируемой величины, которое нужно в данный момент выдерживать, чтобы режим работы регулируемого объекта был наивыгоднейшим. При этом имеется в виду уже не выбор закона регулирования, а автоматический поиск требуемого наивыгоднейшего значения регулируемой величины при изменяющихся внешних условиях работы объекта. Следовательно, на систему, называемую экстремальной, сверх обычной задачи автоматического выдерживания требуемого значения регулируемой величины, накладывается дополнительная задача автоматического поиска наивыгоднейшего значения самого этого требуемого значения регулируемой величины, т. е. самой программы регулирования.
Система экстремального управления предназначена для управления объектами, которые имеют экстремальную статическую характеристику (экстремальный объект).
Система экстремального управления не требует знание мат модели объекта. Т. о. система экстремального управления – частный случай систем оптимального управления, но область применения экстремальных систем намного больше, чем систем оптимального управления.
Структурная схема систем экстремального управления.
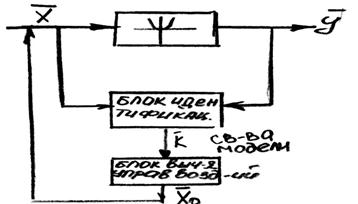
Основное предназначение блока идентификации является не нахождение коэффициентов мат модели, а нахождение конкретных свойств этой модели.
1. Особенности блока идентификации – предназначен для вычислений свойств мат модели.

В системах экстремального управления наиболее часто свойства определяются значением производной в рабочей точки. Знание знака производной является основным определяющим свойством любой экстремальной системы управления и все алгоритмы, которые применяются в блоке идентификации практически направлены на поиски знака производной. В блоке идентификации наиболее часто используются 2 алгоритма:
а) градиентный метод (безмодельный);
б) метод покоординатного поиска (метод пробных шагов).
2. Особенности блока вычисления управляющих воздействий.
Это простой блок, он вычисляет новое управляющее воздействие путем присвоения его к предыдущему:
![]()
А - Выбираем из таблицы
К – находится из блока идентификации
x0 – новое управляющее воздействие (СЛЕДУЮЩЕЕ ПРОЧТИ И УЖАСНИСЬ)
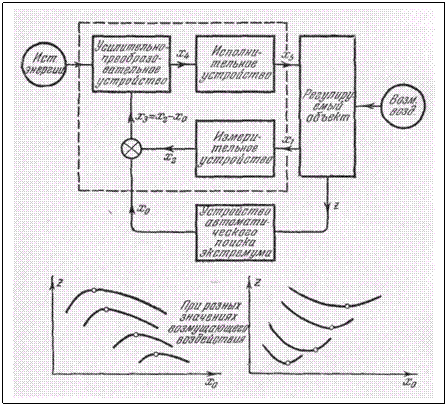
Например, характеристика z (д;0) может быть коэффициентом полезного действия регулируемого объекта (например, двигателя) или величиной расхода горючего в объекте. Тогда устройство автоматического поиска
будет выдавать такое
требуемое значение регулируемой величины ха (например, требуемая скорость вращения
двигателя), которое дает,
соответственно, максимум коэффициента полезного действия или минимум расхода горючего
Рис 237.
При этом как сама величина экстремума 2, так и соответствующее ему значение хй могут существенно меняться в зависимости от внешних условий работы объекта, как показано на рис. 237. Устройство автоматического поиска должно всегда находить этот экстремум независимо от при-
чин,
вызывающих его смещение в процессе работы объекта. Способы такого автоматического поиска
будут описаны ниже. В схеме на рис. 237 в целях наглядности функции автоматического поиска .v0 и измерения фактического значения х1 регулируемой величины разделены. Чаще
же система экстремального
регулирования устраивается так, что обе эти функции объединены в одном приборе, в результате чего устройство автоматического поиска
выдает не х0, а непосредственно разностный сигнал на
усилитель ха,
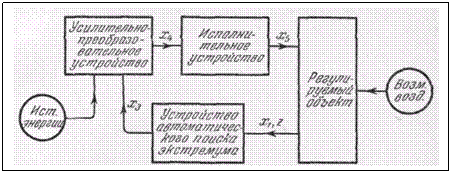
Рис. 238.
пропорциональный отклонению фактического значения регулируемой величины от требуемого для обеспечения экстремума той или иной характеристики регулируемого объекта (рис. 238). Это не меняет общей сути дела.
Экстремальное регулирование может применяться, например, для поддержания наивыгоднейшей скорости полета, соответствующей минимуму расхода горючего на единицу длины пути. При этом будет достигнута и максимальная дальность полета при заданном запасе горючего. Примерами экстремальных систем регулирования могут служить также: автоматическое поддержание максимальной скорости проходки скважины турбобуром при меняющихся свойствах грунта; автоматические системы управления различными производственными процессами, поддерживающие наивыгоднейший режим работы станков; управление энергетическими установками и . системами, обеспечивающее автоматические поиски и поддержание экстремума эксплуатационных характеристик, и т- Д,
Вопрос 14 ТАУ.
Динамические
критерии качества. Классификация, область применения.
![]()
(y1 в 3 раза меньше yд)
Достоинства:
1. Применяется в основном для анализа существующих систем управления.
2. Критерий объективно и достоверно отображает действительную степень затухания колебательного процесса.
Недостаток: Критерий косвенно участвует во многих интегральных критериях.
II. Скорость регулирования – это наибольший угол подъема переходного процесса в начальной стадии.
![]() - скорость переходного
процесса.
- скорость переходного
процесса.
vп.п. применяется в основном для анализа переходного процесса. Он никогда не используется для синтеза СУ, т. к. конфликтует с другим динамическим критерием – временем переходного процесса.
III. Время переходного процесса Tp- это время за которое переходный процесс достигнет заданной статической погрешности.
Время переходного процесса используется для синтеза систем управления как величина, ограничивающая переходный процесс.
IV. Критерий заданной степени колебательности переходного процесса m.
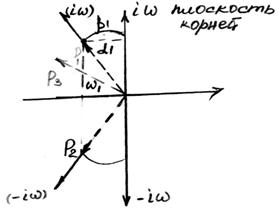

![]()
![]()
Заданная степень колебательности – это угол на который поворачиваются оси определяет плоскость корней до совпадения с первым наиболее близким корнем характеристического уравнения.
Понятие
о расширенных АФХ.
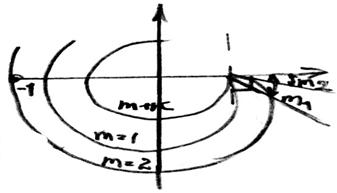

Широко применяются при синтезе систем управления, т.к. широко обеспечивает запас устойчивости синтезированных систем, удобен в применении, поскольку искажает АФХ в нужном направлении.
V. Заданная степень устойчивости применяется в количественном плане.
η – запас устойчивости
равный α1 – действительная часть 1го корня.
Получаем расширенную АФХ.

![]()
Вопрос 15 ТАУ.
Математическое
описание усилительного звена и его характеристики.
1. Математическая модель

y(t)=kx(t)
k-коэффициент усиления (трансформации)
Преобразованная по Лапласу математическая модель
y(t)=kx(t);
y(P)=kx(P)
![]()
2. Динамические характеристики; вывод из передаточной функции. Для этого в передаточной функции производится формальная замена P→i
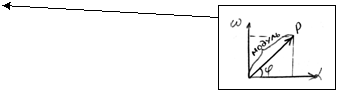 Формула
АФХ - W(i)=k
Формула
АФХ - W(i)=k
P=+ i
Re Im
![]() - АЧХ
- АЧХ
![]() - ФЧХ
- ФЧХ
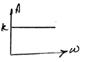
![]()
![]()
На основании АЧХ и ФЧХ строим годограф. Годограф представляет собой точку на реальной оси.

3.
Переходный процесс усилительного звена.
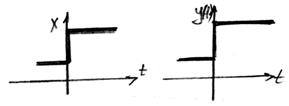
Пример усилительного звена рупор, зубчатая передача,
громкоговоритель.
Вопрос 16 ТАУ.
Нелинейные системы
управления
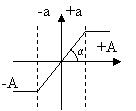
Нелинейной системой называется система у которой управляющее устройство имеет нелинейную статическую характеристику.
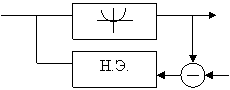
Типы нелинейных элементов
Для нелинейных элементов динамической характеристики не
существует, т.к. все нелинейные элементы характеризуются разрывами первого рода
( производная существует и в точке разрыва равна бесконечности и существует ![]() предел как слева так и
справа).
предел как слева так и
справа).
Нелинейные элементы исследуются только с помощью статической характеристик.
 1.Реле
1.Реле
![]()
Область применения: 80% всех нелинейных элементов обладают релейные элементы (холодильники, стиральные машинки)
2. Реле с гистерезисом (зоной нечувствительности)
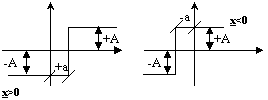

Область применения – 5%
3. Линейно-нелинейные элементы(нелинейные элементы с линейной зоной).
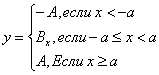
![]()
4. Гистерезисный элемент
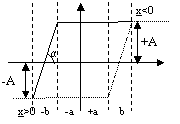

![]()
Вопрос 17 ТАУ.
Метод расчета двухконтурной САУ для случая когда частота внутреннего контура соизмерима с частотой внешнего контура. внут>внеш
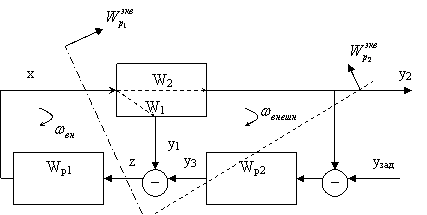
Исходные данные
а) W1,W2
б) структура
W1, W2=> k1+k2/p+k3p
Найти: ![]() - ?
- ?
Алгоритм расчета.
1 шаг. т.к. вн>внешн, то y3≠const
Находим эквивалентную передаточную функцию регулятора WP2экв
![]()
![]() и в этой передаточной функции регулятор WP1 с
коэффициентом 1.
и в этой передаточной функции регулятор WP1 с
коэффициентом 1.
WP1=1,
тогда ![]()
2 шаг По передаточной функции рассчитывается регулятор WP2
WP2экв=>WP2=>(k21’,
k22’, k23’)
3 шаг
Находим WP1экв=W2WP2-W1
4 шаг WP1экв=>WP1=>(k11’,
k12’, k13’)
5 шаг По ![]() рассчитываются
настроечные коэффициенты Wp2=>(k21’’, k22’’, k23’’)
рассчитываются
настроечные коэффициенты Wp2=>(k21’’, k22’’, k23’’)
6 шаг принятие решения об окончании
а) если ![]() , то END
, то END
б) если ![]() , то возвращаемся к шагу 4.
, то возвращаемся к шагу 4.
Вопрос 18 ТАУ
Статические
критерии качества и их применение.
Качество систем управления – это свойство переходных процессов в замкнутых системах управления.
Оценка качества СУ производится по критериям качества. Все критерии качества делятся на 3 группы.
1. Статические критерии – которые оценивают качество переходного процесса СУ в статическом режиме.
2. Динамические критерии – критерии, которые оценивают качество переходного процесса СУ в динамическом режиме (при движении).
3. Интегральные критерии – которые оценивают качество СУ в статике и динамике.
Статические критерии делятся на статическую и динамическую погрешности.
1. Статическая погрешность (D) – называется величина отклонения переходного процесса от задания в момент окончания переходного процесса (т.е. t®µ). Статические погрешности при расчете задаются.
Применяется только для анализа. Критерий статической погрешности для синтеза не применяется, т.к. для создания СУ больше нужна динамика.
Тр-время регулирования технологического процесса. Статическая погрешность - величина отклонения переходного процесса в определенный период времени.
2. Динамическая погрешность (уд).
 Характеризует
максимальный выброс переходного процесса от величины задания. Динамическая
погрешность как и статическая применяется только для анализа СУ.
Характеризует
максимальный выброс переходного процесса от величины задания. Динамическая
погрешность как и статическая применяется только для анализа СУ.
Вопрос 19 ТАУ.
Понятия о
динамических характеристиках объектов и систем автоматического управления.
Все динамические характеристики объетов упраления делется на две группы:
· Весовые, честотные и переходные характеристики
1 Переходной характеристикой называется реакция объекта на вохмушение типа скачок
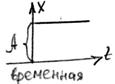

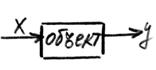
![]() преобразование
Лапласа А(Р)=1/Р
преобразование
Лапласа А(Р)=1/Р
А=1
В случае когда возмущение на входе =1 переходная функция называется кривой разгона.
Зная переходную функцию всегда можно восстановить то дифференциальное уравнение которое описывается объект управления (вытекает из того, что переходная функция является решение дифференциальным уравнением).
2. Весовой функцией называется реакция объекта на импульсное возмущение

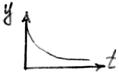
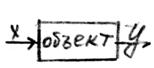
Функция Дирака (t) импульсного возмущения называется функция следующего вида:
![]()
![]()
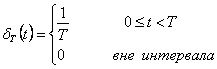
![]()
1. Функция это частный случай переходного процесса
2. Весовая функция g(t) это комбинация двух решений: прямого и обратного.
3. g(t) есть производная от переходной функции h(t).
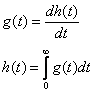 основное свойство,
связывать основную функцию с переходной функцией
основное свойство,
связывать основную функцию с переходной функцией
![]()
 интеграл
свертки двух функций (Дюамель).
интеграл
свертки двух функций (Дюамель).
Если известно![]()
![]()
![]()
![]()
4. Частотные характеристики – это характеристики которые показывают объект либо системы в зависимости от частоты (от скорости изменения сигнала).

Амплитудно-частотная характеристика – это зависимость отношения амплитуды выходного сигнала к амплитуде выходного сигнала от частоты.
![]()
Авх=const.
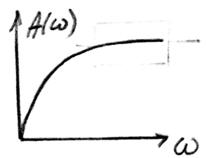
Фазочастотная характеристика- это зависимость разности фазы выходного сигнала и фазы входного сигнала от частоты.
![]()

АЧХ
Амплитуднофазочастотная характеристика АФХ- предстовляет собой
совмещение комплексной плоскости АЧХ и ФЧХ.
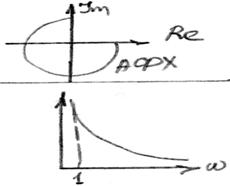

Задаваясь последовательно значение ![]() находится число модуля
(длинны вектора) и угол поворота.
находится число модуля
(длинны вектора) и угол поворота.
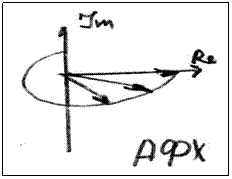 При
При
![]() =0 вектор лежит на реальной оси.
=0 вектор лежит на реальной оси.
АФХ- это годограф вектора длина который изменяется в зависимости от АЧХ а угол поворота в зависимости от ФЧХ.
Вопрос 20 ТАУ
Метод расчета
настроек ПИД управляющего устройства.
В ряде случаев качество
регулирования можно повысить введением в закон регулирования составляющей,
пропорционально первой производной или скорости изменения входной величины
регулятора. Эта дифференциальная составляющая ( Д-составляющая ) формируется
при помощи дополнительного устройства.
Типовой
пропорционально-интегрально-дифференциальный регулятор является более сложным,
чем предыдущие регуляторы. Выражение для его закона регулирования имеет вид:
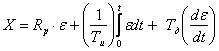
Изменение выходной величины
пропорционально-интегрально-дифференциальных регуляторов пропорционально
отклонению регулируемой величины от заданного значения, интегралу и
производной этого отклонения.
Тд – время
дифференцирования, характеризующее степень влияния скорости изменения ε на
выходную величину х регулятора.
Rp, Ти и Тд
– настроечные параметры пропорционально-интегрально-дифференциального
регулятора.
Структурная схема пропорционально-интегрально-дифференциального
регулятора.

![]() +
+
У _ Х
Схема состоит из
усилительного звена с очень большим коэффициентом передачи (k1>>1)
и апериодического звена первого порядка, установленного в цепи отрицательной
обратной связи. Передаточная функция
W(p) такой
системы равна :
W(p)=
Пропорционально-интегрально-дифференциальный
регулятор применяют тогда, когда объекты характеризуются большим запаздыванием
и претерпевают значительные изменения – нагрузки.
Расчет
пропорционально-интегрально-дифференциального закона регулирования.
Исходные данные: A(ω)
F(ω)
Алгоритм расчета:
Расчет ведем по расширенным
параметрическим функциям:
Расширение проводим по
заданной степени колебательности (затухания) –m.
![]()
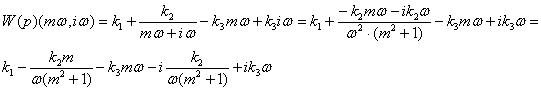 (5)
(5)
![]()
Мнимая параметрическая
функция φ – это мнимая часть расширенной амплитудно-фазовой
характеристики регулятора.
Расширенной
амплитудно-фазовой характеристикой называют искуственное изменение за счет введения
дополнительных параметров амплитуднофазовой характеристики.
В формуле (5) прибавим и
отнимем k3mω.
![]()
![]()
Записываем
систему Найквиста-Михайлова.
![]() Ар·Ао=1
Ар·Ао=1
Fp+Fo=0
Строим
амплитуднофазочастотную характеристику, при этом задавшись некоторым значением φ.
Re=F+mφ => F=Re-mφ
Задаемся
следующим значением частоты ω.
![]()
Fp=-F0
Строим
амплитудно-фазо-частотную характеристику используя φ.
Re=F+mφ => F=Re-mφ
Задаемся
еще одним значением частоты ω
![]()
![]() ;
;
Fp=-Fo;
Строим амплитудно-фазо-частотную характеристику
Re=F+mφ; F=Re-mφ
Строим
плоскость параметрических функций.
Плоскость
параметрических функций – это
геометрическое место точек равных заданной степени колебательности m, построенное в координатах параметрических функций.
Плоскость
параметрических функций
Из
плоскости находим оптимальную рабочую частоту.
Составляем
систему уравнений:
φmax=k3·ωmax-![]()
Fmax=k1-2k3m ωmax
Решаем
систему уравнений относительно k1,k2,k3 методом последовательных приближений.
Для
этого задаемся любым значением k1, решаем систему уравнений относительно k2,k3
Если
0,25![]() , то расчет заканчиваем.
, то расчет заканчиваем.
Если
![]() >0,75, то расчет повторим, уменьшив k1 на
10%.
>0,75, то расчет повторим, уменьшив k1 на
10%.
Если
![]() <0,25, то расчет повторим, увеличив k1 на
10%.
<0,25, то расчет повторим, увеличив k1 на
10%.
Если
найденное значение попадает вдиапазон от 0,25 до 0,75, то расчет заканчиваем.
21.ТАУ
Математическое описание цифровых типовых звеньев и их характеристики
АЦП
Через равный промежуток времени t

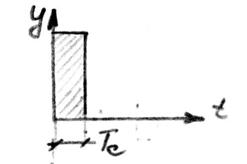
Ts-расстояние между двумя импульсами
1.мат. модель 
2. Передаточная функция: импульс разбивает на два скачка и от них берут преобразование Лапласа:


где Tc-ширина импульса
Общая передаточная функция:
![]()
3. Динамические харакеристики:
![]()
![]()
![]()
3.1 АФХ : ![]()
3.2 АЧХ 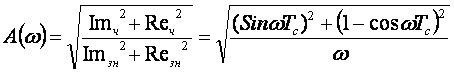

3.3 ФЧХ 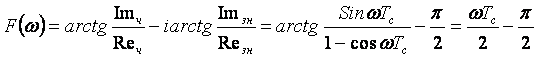
3.4 Годограф АФХ
Область применения: служит для соединения аналоговых частей функциональных схем (приборы, блоки, средства автоматизации) с цифровыми и микропроцессорной техникой).

ЦАП

ЦАП “
ЦАП “1”и более
Равные промежутки
Чтобы найти математическую модель рассмотрим единичный импульс со следующими параметрами
1. математическая модель

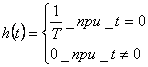
2. Передаточная функция =Ts
По Лапласу: y1(p)=1/p ; ![]()
![]()
3. Динамические характеристики
p→i ![]()
![]()
АФХ: ![]()
АЧХ: 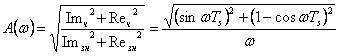
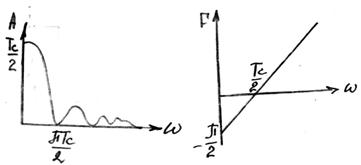
ФЧХ: ![]()
Годограф

Вопрос 22 ТАУ
Метод
расчета настроек ПИ-управляющего устройства.
Исходные
данные
1. Динамические характеристики объекта в приближенном виде (передаточная функция , АЧХ, либо ФЧХ).
2. Необходимо знать динамические характеристики регулятора хотя бы в приближенном виде.
3. Необходимо знать критерий устойчивости Найквиста-Михайлова
4. Необходимо что бы среднеквадратический критерий →к min
Алгоритм расчета
1. Составляется система уравнении Найквиста-Михайлова для конкретных значений регулятора и объекта.
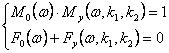 (1)
(1)
Для решения системы существует следующий алгоритм.
а) Подставляем =1 система уравнений решается относительно k1 k2. Полученные значения в виде точки заносятся в так называемую плоскость настроек.
Понятия о
плоскости настроек
Плоскостью настроек называется график зависимости интегральной настройки регулятора от пропорциональной.
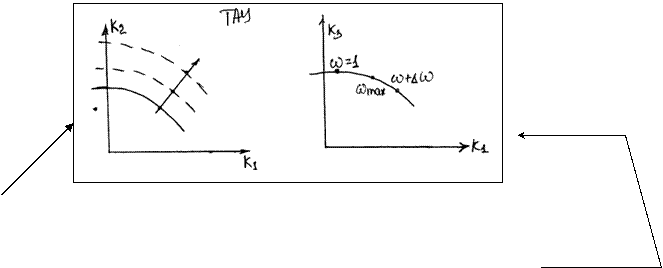
Максимальное значение плоскости настроек соответствует минимальному среднеквадратическому критерию качества и зависит от степени колебательности. Чем больше m тем больше этот максимум смещается вправо и вверх.
б) Задается приращение частоты и подставляется в систему уравнений (1). Находят следующую точку в плоскости настроечных коэффициентов до тех пор, пока не будет найден перегиб.
в) Затем находят рабочую частоту по формуле:![]()
Умножение на коэффициент необходимо для придания системе большей устойчивости.
г) Полученное значение рабочей частоты подставляется в систему уравнений Найквиста – Михайлова и найденные коэффициенты k1раб и k2раб подставляются в передаточную функцию пропорционально – интегрального регулятора.
Достоинства метода:
1) Метод позволяет увязать критерий устойчивости и качества.
2) Метод легко формализуем.
3) Метод дает хорошие результаты с точки зрения практики, т.ее является помехоустойчивым.
Недостаток: метод грешит эмпирическими допущениями. Коэффициент 0,9 при расчете раб получен опытным путем и с математической точки зрения не объяснен.
Вопрос 23 ТАУ
Системы
оптимального управления (СОУ) и их особенности.
Предназначены для управления объектами, имеющими нелинейные статические характеристики и линейные динамические характеристики. Статические характеристики объекта должны быть экстремальными (иметь ярко выраженный максимум или минимум).
Структурная схема СОУ
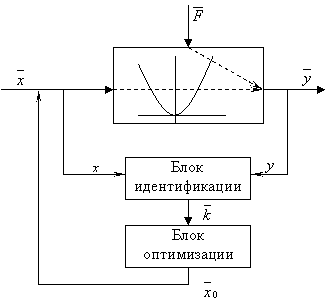
Такая система не реализуется на обычных аналоговых звеньях. Для реализации СОУ необходима вычислительная техника: блок идентификации и блок оптимизации, т.к. они являются программными блоками.
Структура
блока идентификации: предназначен для постоянного отслеживания
коэффициентом заданий мат. модели. Связан с методом наименьших квадратов,
который постоянно рассчитывает выходные значения мат модели и сравнивает их со
значениями которые на выходе объекта. (Алгоритм решения) Δ=yp-yэ; yp(![]() ) – по мат. модели.; yэ –
экспериментально;
) – по мат. модели.; yэ –
экспериментально; ![]()
При минимизации этого функционала используется метод градиентного поиска. Метод, когда на управляющие воздействия наложены ограничения штрафных функций; Метод координатного поиска (метод Гаусса - Зейделя).
Особенности функционирования блока оптимизации.
1. Для решения задач оптимизации используется метод по координатного поиска.
2. Метод Гаусса – Зейделя (градиентный метод).
3. В тех случаях когда на входные параметры объекта наложены ограничения используется метод штрафных функций.
Эти алгоритмы предназначены для решения заранее заданной мат. модели.
24.ТАУ
Метод
расчета настроек П – управляющего устройства.
Исходные
данные
а) Известна передаточная функция W0(p)
б) Структура регулятора Wр(p)=k1
Алгоритм синтеза:
1. Из передаточной функции объекта выделяем АЧХ и ФЧХ объекта.
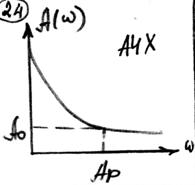
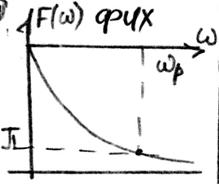
2)
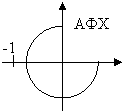 Выбираем
критерий синтеза. Обычно при синтезе применяется критерий устойчивости
Найквиста – Михайлова
Выбираем
критерий синтеза. Обычно при синтезе применяется критерий устойчивости
Найквиста – Михайлова
W0-Wp=1
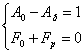
3. Выделяем известные параметры регулирующего устройства.
ФЧХр=
. Поиск k1
а) находим рабочую частоту системы р
б) находим амплитуду регулирования ![]() при р=> Ap= k1
при р=> Ap= k1
Метод расчета настроек П-управляющего устройства.
Исходные данные
1. Динамичесике характеристики объекта в приблмженном виде (передаточная функция , АЧХ, либо ФЧХ).
2. Необходимо знать динамические характеристики регулятора хотябы в приближеноом виде.
3. Необходимо знать критерий устойчивости Найквиста-Михайлова
4. Необходимо что бы среднеквадратический критерий →к min
Алгоритм расчета
1. Составляется система уравнении Найквиста-Михайлова для конкретных значений регулятора и объекта.
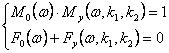 (1)
(1)
Вопрос 25 ТАУ
Метод расчета 2х контурной системы управления для случая когда частота внутреннего контура много больше частоты внешнего контура.
![]()
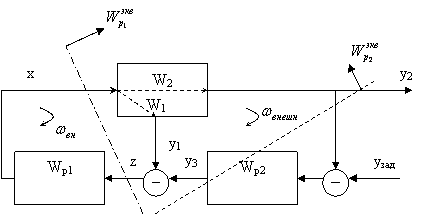
Исходные данные:
1. W1(p), W2(p)-известны
2.
структура ![]()
Найти: ![]()
Алгоритм расчета.
1) т.к. ![]() , то у3=const по отношению к у1
, то у3=const по отношению к у1
Рассчитывается W1р по передаточной функции W1 (различные законы: П, ПИ, ПИД, …)
Известны ![]()
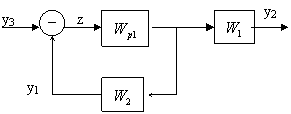 2)
Находим эквивалентную передаточную функцию объекта, которым управляет второй
регулятор W2.
Все что находится выше линии - - - - - является эквивалентным регулятором
2)
Находим эквивалентную передаточную функцию объекта, которым управляет второй
регулятор W2.
Все что находится выше линии - - - - - является эквивалентным регулятором ![]()
![]()
3) Рассчитывается регулятор Wp2 по
передаточной функции ![]() любым законом.
любым законом.
![]() 2 – номер регулятора;
1 – номер настройки;
2 – номер регулятора;
1 – номер настройки;
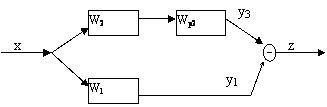 4)
Нахождение эквивалентной передаточной функции которой управляет регулятор Wp1
(отсекаем -·-·-·-·-·-).
4)
Нахождение эквивалентной передаточной функции которой управляет регулятор Wp1
(отсекаем -·-·-·-·-·-).
![]() векторная
форма.
векторная
форма.
5) Рассчитываем регулятор №1 W1 по передаточной функции ![]()
![]()
6) Принятие решения об окончании расчета. Сравниваются коэффициенты пропорциональной настройки:
а) Если ![]()
б) Если ![]()
Вопрос 26 ТАУ
Критерий
устойчивости Михайлова; следствия из критерия; привести пример исследования
устойчивости САУ данным критерием.
Область применения: в электрике, электронике, автоматике т.к. основной используемой характеристикой для принятия решений является АФХ.
Характеристическое уравнение: 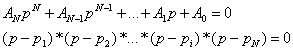
pi=1…N – корни характеристического уравнения pi=a±iw.
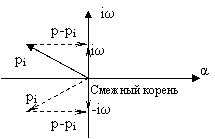 DF=N*p.
DF=N*p.
Критерий Михайлова: Если суммарный прирост фазочастотной характеристики при изменении частоты от -µ до +µ равен N*p, где N – число корней характеристического уравнения, то система является устойчивой.
Первое
следствие из теоремы Михайлова по ФЧХ: ![]()
САУ будет устойчива, если годограф Михайлова поворачивается
на угол ![]() при изменении частоты
от 0 до +µ;
N – число корней
характеристического уравнения.
при изменении частоты
от 0 до +µ;
N – число корней
характеристического уравнения.
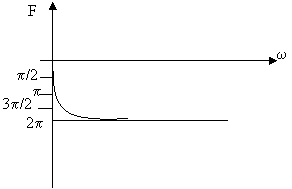
N=2 – устойчивое
N=3; 7… - неустойчивое
Второе следствие из критерия Михайлова по АФХ.
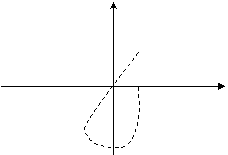
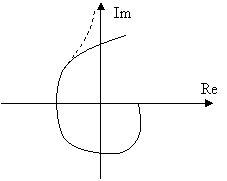 САУ будет устойчива, если АФХ
объекта последовательно обходит N
квадрантов плоскости комплексных переменных при изменении частоты от 0 до +µ, гд N – число корней
характеристического уравнения.
САУ будет устойчива, если АФХ
объекта последовательно обходит N
квадрантов плоскости комплексных переменных при изменении частоты от 0 до +µ, гд N – число корней
характеристического уравнения.
![]()
![]() N=4 – ( ) устойчивая
N=4 – ( ) устойчивая
( ) неустойчивая
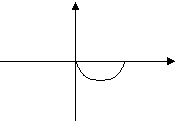
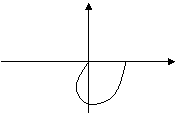
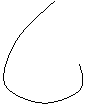
Третье следствие из критерия Михайлова по АЧХ и ФЧХ:Система
управления будет устойчива, если корни мнимой и действительной частей АФХ
системы чередуются, при изменении частоты от 0 до +µ.
![]()
![]()
N=4 устойчив.
![]()
Преимущества:1)Критерий Михайлова многогранен и имеется возможность принятия решения отдельно по ФЧХ, отдельно по АФХ и частей АФХ.2) Простота принятия решений.3) Надежность и достоверность принятия решений.
Недостатки:1) Очень сложно принять решения, если АФХ нужно
строить самим.2) Практически невозможно применять критерии Михайлова для
исследования устойчивости замкнутых САР или отрицательных обратных связей. В
связи с этим в теории автоматического
управления критерий Михайлова используют для анализа и исследования существующих
САУ и невозможность его управления для синтеза системы.


Вопрос 27 ТАУ
Понятие об адаптивных системах управления.
Адаптивные, или приспосабливающиеся, системы — это системы, которые автоматически приспосабливаются к изменению внешних условий и свойств объекта управления, обеспечивая при этом необходимое качество управления путем изменения структуры и параметров управляющего устройства.
Качество управления численно определяется критерием качества, который оценивает заранее выбранный наиболее важный показатель работы САУ. Им может быть какой-либо показатель точности работы системы или качества переходного процесса, производительность, экономичность и т. д. В общем случае критерий качества представляет собой функционал, зависящий от выходных и входных величин системы, подобно критерию оптимальности в оптимальных САУ.
Примером изменяющихся внешних условий, требующих применения адаптивной САУ, являются нестационарные случайные внешние воздействия на систему, характеристики которых (например, спектральная плотность) изменяются в широких пределах. В этих условиях точность работы САУ будет изменяться с изменением статистических характеристик внешних воздействии (см. третью главу). Для повышения точности системы необходимо изменять настройку корректирующих звеньев по мере изменения характеристик внешних воздействий. Эту перенастройку иногда
может выполнять человек. В адаптивных САУ она осуществляется автоматически.
|
|
Примером объекта с переменными параметрами, также требующего адаптивного управления, является самолет или ракета. Их динамические характеристики могут изменяться со временем в очень широких пределах вследствие изменения массы из-за уменьшения запаса горючего, изменения формы объекта или аэродинамических сил при изменении высоты и скорости полета. В этих случаях часто невозможно обеспечить автоматическое управление объектом во всех его режимах работы без изменения настройки или схемы управляющего устройства. Для автоматического выполнения этой задачи используются адаптивные САУ.
Помимо объектов с переменными свойствами и внешними условиями, областью применения адаптивных систем являются также объекты с недостаточно известными свойствами или условиями работы. В этом случае процесс адаптации может быть однократным.
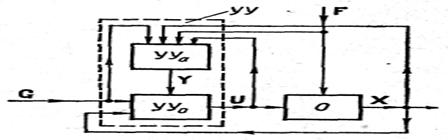
На рис. показана в общем виде схема адаптивной САУ. Здесь О — объект управления, У У — управляющее устройство, состоящее из двух частей: УУ0 и УУа, где УУ0 — основное управляющее устройство, а УУа — управляющее устройство адаптации.
Контур, образованный УУ0 и О, является основным контуром системы и представляет собой обычную неадаптивную САУ. Управляющее устройство адаптации УУа управляет основным управляющим устройством УУ0, изменяя его оператор, т. е. схему и значения параметров, в соответствии с изменением внешних условий работы и свойств объекта. Для этого УУа измеряет в самом общем случае внешние воздействия G и F и выходную и входную величины объекта X и U. По этим данным определяется значение критерия качества управления (X, U, G, F). В зависимости от алгоритма работы устройство УУа определяет отклонение критерия качества от заданного или от экстремального его значения и воздействует на УУ0 так, чтобы ликвидировать это отклонение. Причиной изменения критерия качества может быть изменение внешних условий работы в виде изменений каких-либо характеристик воздействий G и F или изменение свойств основного контура, т. е. операторов объекта О и основного управляющего устройства У У 0.
Таким образом, адаптивная САУ содержит два контура управления — основной контур и второй контур — контур адаптации, создаваемый управляющим устройством адаптации УУа. Для этого второго контура объектом управления является вся основная САУ.
Контур адаптации образует второй уровень управления, второй этаж над основной САУ. Возможен и следующий уровень адаптации, когда управляющее устройство адаптации УУа, в свою очередь, подстраивается, изменяется следующим управляющим устройством, которое при изменении внешних условий или свойств первичной адаптивной САУ изменяет алгоритм адаптации, осуществляемой УУа. Аналогично возможны многоступенчатые САУ, содержащие большее число уровней адаптации. У таких САУ каждый последующий уровень управляет предыдущим, расширяя диапазон условий, при которых система будет правильно выполнять свою задачу, или повышая качество ее выполнения в заданном диапазоне.
Как и всякое управление, автоматическая адаптация, выполняемая управляющим устройством УУа, принципиально может быть осуществлена в виде разомкнутой, замкнутой и в самом общем случае комбинированной системы. На рис. показан этот последний случай.
При разомкнутой цепи адаптации управляющее устройство УУЯ не образует замкнутого контура. Как обычно, разомкнутое управление осуществляется здесь либо как программное управлений основным управляющим устройством УУ0 в функции времени, либо как система компенсации, действующая в функции внешних воздействий G или F, Первый вариант адаптации предполагает наличие заданного графика изменения во времени характеристик основной САУ или внешних воздействий.
Адаптация, осуществляемая с помощью замкнутого контура, т. е. с обратной связью, действует в функции выходной величины X объекта и, возможно, также выходной величины U основного управляющего устройства.
Как и у обычных САУ, основным типом адаптивных САУ является замкнутая система адаптации. Поэтому везде в дальнейшем под адаптивными САУ имеются в виду именно замкнутые адаптивные САУ. Применение при этом компенсационных сигналов по внешним воздействиям представляет собой вспомогательное средство повышения качества адаптации и упрощения управляющего устройства.
Система адаптации, точнее управляющее устройство УУа, может работать постоянно, периодически (включаясь через определенные интервалы времени) и однократно (путем подключения вручную к САУ для осуществления ее автоматической настройки). Адаптивные САУ делятся на САУ со стабилизацией и с оптимизацией качества управления. Задачей САУ со стабилизацией качества управления является удержание критерия качества управления на определенном уровне или в определенном диапазоне. Контур адаптации выполняет здесь задачу стабилизации этого критерия. В С А У с оптимизацией качества управления обеспечивается поиск и поддержание оптимального значения критерия качества.
По характеру изменений в основном управляющем устройстве УУ0, производимых управляющим устройством УУа в процессе адаптации, адаптивные системы делятся на самонастраивающиеся и самоорганизующиеся. В самонастраивающихся САУ адаптация осуществляется изменением значений параметров основного управляющего устройства УУ0, а в самоорганизующихся САУ изменяется структура УУ0.
Область применения адаптивных САУ
– это управление объектами, свойства или условия работы которых недостаточно
известны или существенно непостоянны. В этих условиях обыкновенная,
неадаптивная система либо будет работать неудовлетворительно, либо потребует
постоянного надзора.
28 ТАУ. Понятия о
компенсации в системах управления.
Основным признаком компенсации возмушений САУ является синтез компенсатора, который убирает с объекта управления.
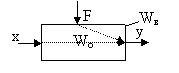
1. Система объекта по возмущению необходимы тогда когда объект имеет несколько входных сигналов и один выходной.
2. У системы компенсации по возмущению часть параметров не имеет возможности быть управляемыми.
Существуют два принципа компенсации возмущения: а) по возмущению; б) по отклонению.
1. Принцип компенсации по возмущению заключается в том, что находят такое дополнительное тех. Устройство (компенсатор), связывающее возмущающее воздействие и один из управляющих входов которые позволяют полностью или частично уничтожить влияние передаточной функции по каналу возмущения Wв.
Структурная схема выгладит так:
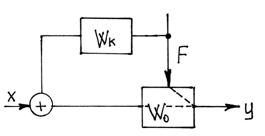
Системы с компенсацией по возмущению не имеет регуляторов с обратной связью с объектом, функции регулятора выполняет компенсатор.
Синтез компенсатора по возмущению.
А) Исходные данные: Wo и Wи. Наитии Wk.
Б) ![]()
Передаточная функция компенсатора![]() все зависит от знака.
все зависит от знака.
Условия физической реализуемости компенсаторов и способы их достижения.
1.
Передаточная функция физически реализуемого звена
(компенсатора) не должна содержать элементов упреждения ![]() . Для достижения физической реализации в полученной
передаточной функции компенсатора звенья упреждения убираются.
. Для достижения физической реализации в полученной
передаточной функции компенсатора звенья упреждения убираются.
2. Система будет физически реализуема, если порядок характеристического уравнения в числителе передаточной функции компенсатора будет ≤ порядка характеристического уравнения в знаменателе. Степень полинома числителя-N
Степень полинома знаменателя-M
N≥M
Если N>M тогда передаточная функция компенсатора получилось физически не реализуемой по второму условию, следовательно, для достижения физической реализуемости степень полинома числителя снижают до тех пор, пока она не станет, равна степени полинома знаменателя.
Способ компенсации по отклонению
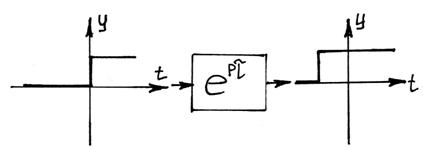
Составляются уравнения равновесия, упрощается, лишнее отбрасывается.
Часть сигнала y: FWв
![]()
Передаточная функция компенсатора:![]()
Проверка физической реализуемости производится двумя
способами рассмотренными выше.
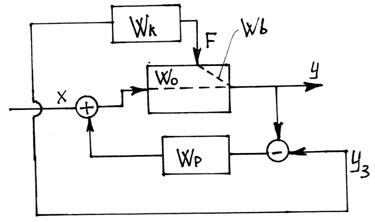
Вопрос 29 ТАУ математическое описание апериодического звена и его характеристики.
1. Мат. модель: линейное диф. звено первого порядка
![]() Т1-постаянная
времени
Т1-постаянная
времени
передаточная функция: преобразование по Лапласу
![]()
![]() оператор Лапласа
оператор Лапласа
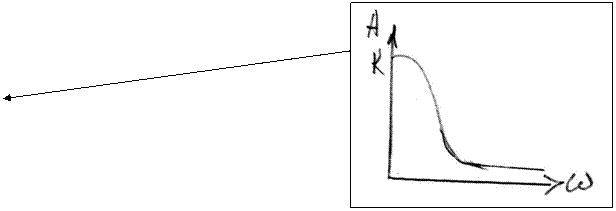
2. Передаточная функция –это отношение преобразованного по Лапласу выходного сигнала к преобразованному по Лапласу входному сигналу
![]()
3. Динамические характеристики апереодического звена
3.1. АФХ ![]()
![]()
3.2. АЧХ
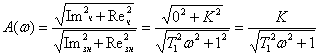
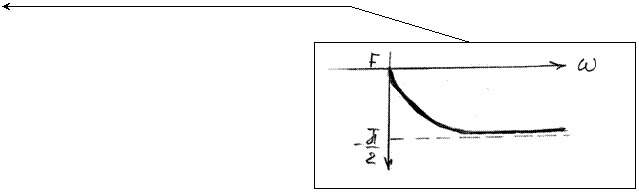 3.3.
ФЧХ
3.3.
ФЧХ
![]()
«-» - построение АФХ идет по часовой стрелке
3.4. Построение годографа -построение от К до 0
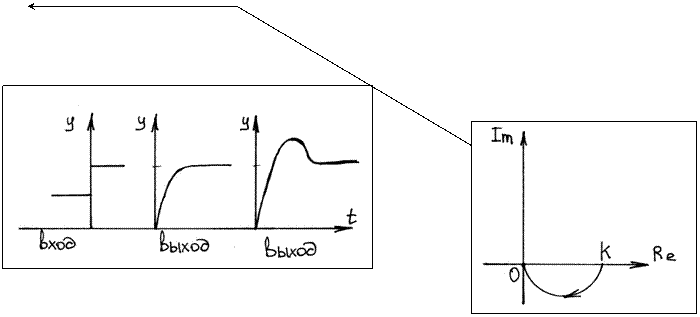
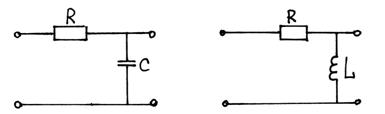
3.5. Переходная функция
Пример:
Вопрос 30 ТАУ
Понятие
управляемости, наблюдаемости и робастности систем управления
Управляемость
Для решения задач управления важно знать, обладает ли объект свойством управляемости в смысле возможности его перевода из заданной начальной точки (или области) в заданную конечную точку (или область).В сложных случаях не исключена ошибка в выборе структуры системы управления, из-за чего объект не будет обладать указанным свойством. Поэтому возникает проблема управляемости — проблема установления обладания объектом свойства управляемости.
Перейдем к строгому определению свойства управляемости объекта и установлению критерия управляемости.
Пусть объект задается уравнением
![]() = f (x, u, t), Любой х из множества Rn, Любой u из множества Rr.
= f (x, u, t), Любой х из множества Rn, Любой u из множества Rr.
Здесь пока принимается, что допустимое множество Ut значений управления совпадает со всем пространством Rr и допустимым управлением является любая кусочно-непрерывная вектор-функция, принимающая значения из Rr.
Объект называется вполне или полностью управляемым, если для любой пары точек х° и хf из Rn существует допустимое управление на конечном интервале [t0, tf], переводящее объект из точки х (t0) = х° в точку x (tf) = хf.
30. Понятие
управляемости, наблюдаемости и робастности систем управления.
Многосвязный объект – объект, у которого есть n входов и m выходов, связанных между собой. В общем случае m≠n, и в этом случае приводят к случаю m=n, т.к. все методы исследования многосвязных систем управления основаны на теории матриц. Многосвязные системы анализируются с помощью матричных моделей – способ математического описания объекта в пространстве состояний. Элементы матрицы – это передаточные функции отдельных каналов. В общем случае это матрица MxN – матрица пространства состояний.

Если в матрице занята только диагональ (а все другие элементы =0), то имеем только прямые связи, т.е. берется каждый канал в отдельности, и под него синтезируется своя одноконтурная САР. Такие САР называют еще автономными.
Если же элементы главной диагонали равны 0, то эта САР – управляемая.
Если в матрице нет нулей, то САР называют абсолютно наблюдаемой.
Если в матрице есть хотя бы 1 нулевой элемент, то САР называется частично наблюдаемой.
Степень наблюдаемости определяется в процентах:
Н = (кол-во_всех_эл-тов – кол-во_нулей) / кол-во_всех_эл-тов
Робастность оценивается по количеству нулевых элементов матрицы:
R = кол-во_нулей / кол-во_всех_эл-тов
С помощью понятия робастности оценивают грубость создаваемой САР.